Z Wikipedii, wolnej encyklopedii
Ten artykuł należy dopracować: wykresy. Dokładniejsze informacje o tym, co należy poprawić, być może znajdują się w dyskusji tego artykułu . Po wyeliminowaniu niedoskonałości należy usunąć szablon {{Dopracować}} z tego artykułu.
rozkład χ
Gęstość prawdopodobieństwa
Parametry
A , B , ν
Gęstość prawdopodobieństwa
f
(
x
)
=
(
x
−
A
B
)
ν
−
1
e
−
1
2
(
x
−
A
B
)
2
2
ν
2
−
1
B
Γ
(
ν
2
)
{\displaystyle f(x)={\frac {\left({\frac {x-A}{B}}\right)^{\nu -1}e^{-{\frac {1}{2}}\left({\frac {x-A}{B}}\right)^{2}}}{2^{{\frac {\nu }{2}}-1}B\Gamma \left({\frac {\nu }{2}}\right)}}}
Dystrybuanta
F
(
x
)
=
Γ
(
ν
2
,
1
2
(
x
−
A
B
)
2
)
{\displaystyle F(x)=\Gamma \left({\frac {\nu }{2}},{\frac {1}{2}}\left({\frac {x-A}{B}}\right)^{2}\right)}
Wartość oczekiwana (średnia)
A
+
2
B
Γ
(
ν
+
1
2
)
Γ
(
ν
2
)
{\displaystyle A+{\frac {{\sqrt {2}}B\Gamma \left({\frac {\nu +1}{2}}\right)}{\Gamma \left({\frac {\nu }{2}}\right)}}}
Mediana
nie może być wyrażona za pomocą funkcji elementarnych
Moda
A
+
B
ν
−
1
{\displaystyle A+B{\sqrt {\nu -1}}}
Wariancja
B
2
[
ν
−
2
Γ
2
(
ν
+
1
2
)
Γ
2
(
ν
2
)
]
{\displaystyle B^{2}\left[\nu -{\frac {2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\Gamma ^{2}\left({\frac {\nu }{2}}\right)}}\right]}
Współczynnik skośności
2
[
4
Γ
3
(
ν
+
1
2
)
+
Γ
2
(
ν
2
)
(
2
Γ
(
ν
+
3
2
)
−
3
ν
Γ
(
ν
+
1
2
)
)
]
Γ
3
(
ν
2
)
[
ν
−
2
Γ
2
(
ν
+
1
2
)
Γ
2
(
ν
2
)
]
3
2
{\displaystyle {\frac {{\sqrt {2}}\left[4\Gamma ^{3}\left({\frac {\nu +1}{2}}\right)+\Gamma ^{2}\left({\frac {\nu }{2}}\right)\left(2\Gamma \left({\frac {\nu +3}{2}}\right)-3\nu \Gamma \left({\frac {\nu +1}{2}}\right)\right)\right]}{\Gamma ^{3}\left({\frac {\nu }{2}}\right)\left[\nu -{\frac {2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\Gamma ^{2}\left({\frac {\nu }{2}}\right)}}\right]^{\frac {3}{2}}}}}
Kurtoza
2
ν
(
1
−
ν
)
Γ
4
(
ν
2
)
−
24
Γ
4
(
ν
+
1
2
)
[
ν
Γ
2
(
ν
2
)
−
2
Γ
2
(
ν
+
1
2
)
]
2
+
{\displaystyle {\frac {2\nu (1-\nu )\Gamma ^{4}\left({\frac {\nu }{2}}\right)-24\Gamma ^{4}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}+}
+
8
(
2
ν
−
1
)
Γ
2
(
ν
2
)
Γ
2
(
ν
+
1
2
)
[
ν
Γ
2
(
ν
2
)
−
2
Γ
2
(
ν
+
1
2
)
]
2
{\displaystyle +{\frac {8(2\nu -1)\Gamma ^{2}\left({\frac {\nu }{2}}\right)\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}}
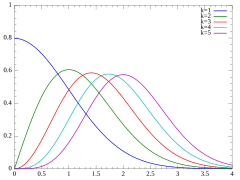
Rozkład chi (zapisywany jako rozkład χ) to rozkład prawdopodobieństwa typu ciągłego.
Funkcja gęstości prawdopodobieństwa tego rozkładu dana jest wzorem:
f
(
x
)
=
(
x
−
A
B
)
ν
−
1
e
−
1
2
(
x
−
A
B
)
2
2
ν
2
−
1
B
Γ
(
ν
2
)
,
{\displaystyle f(x)={\frac {\left({\frac {x-A}{B}}\right)^{\nu -1}e^{-{\frac {1}{2}}\left({\frac {x-A}{B}}\right)^{2}}}{2^{{\frac {\nu }{2}}-1}B\Gamma \left({\frac {\nu }{2}}\right)}},}
gdzie
A
,
B
,
ν
{\displaystyle A,B,\nu }
funkcję gamma .
Parametr
ν
{\displaystyle \nu }
liczbą stopni swobody rozkładu, musi być liczbą większą od 0.
Dystrybuanta tego rozkładu ma postać:
F
(
x
)
=
Γ
(
ν
2
,
1
2
(
x
−
A
B
)
2
)
.
{\displaystyle F(x)=\Gamma \left({\frac {\nu }{2}},{\frac {1}{2}}\left({\frac {x-A}{B}}\right)^{2}\right).}
Własności:
skośność:
2
[
4
Γ
3
(
ν
+
1
2
)
+
Γ
2
(
ν
2
)
(
2
Γ
(
ν
+
3
2
)
−
3
ν
Γ
(
ν
+
1
2
)
)
]
Γ
3
(
ν
2
)
[
ν
−
2
Γ
2
(
ν
+
1
2
)
Γ
2
(
ν
2
)
]
3
2
{\displaystyle {\frac {{\sqrt {2}}\left[4\Gamma ^{3}\left({\frac {\nu +1}{2}}\right)+\Gamma ^{2}\left({\frac {\nu }{2}}\right)\left(2\Gamma \left({\frac {\nu +3}{2}}\right)-3\nu \Gamma \left({\frac {\nu +1}{2}}\right)\right)\right]}{\Gamma ^{3}\left({\frac {\nu }{2}}\right)\left[\nu -{\frac {2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\Gamma ^{2}\left({\frac {\nu }{2}}\right)}}\right]^{\frac {3}{2}}}}}
kurtoza:
2
ν
(
1
−
ν
)
Γ
4
(
ν
2
)
−
24
Γ
4
(
ν
+
1
2
)
[
ν
Γ
2
(
ν
2
)
−
2
Γ
2
(
ν
+
1
2
)
]
2
+
{\displaystyle {\frac {2\nu (1-\nu )\Gamma ^{4}\left({\frac {\nu }{2}}\right)-24\Gamma ^{4}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}+}
+
8
(
2
ν
−
1
)
Γ
2
(
ν
2
)
Γ
2
(
ν
+
1
2
)
[
ν
Γ
2
(
ν
2
)
−
2
Γ
2
(
ν
+
1
2
)
]
2
{\displaystyle +{\frac {8(2\nu -1)\Gamma ^{2}\left({\frac {\nu }{2}}\right)\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}}
Specjalne przypadki:
Rozkłady statystyczne
Rozkłady ciągłe
Rozkłady dyskretne





![{\displaystyle B^{2}\left[\nu -{\frac {2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\Gamma ^{2}\left({\frac {\nu }{2}}\right)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aad4d6f4a2afe31660064f221562081f8accfa7)
![{\displaystyle {\frac {{\sqrt {2}}\left[4\Gamma ^{3}\left({\frac {\nu +1}{2}}\right)+\Gamma ^{2}\left({\frac {\nu }{2}}\right)\left(2\Gamma \left({\frac {\nu +3}{2}}\right)-3\nu \Gamma \left({\frac {\nu +1}{2}}\right)\right)\right]}{\Gamma ^{3}\left({\frac {\nu }{2}}\right)\left[\nu -{\frac {2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\Gamma ^{2}\left({\frac {\nu }{2}}\right)}}\right]^{\frac {3}{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce69ba66d5c37168808887c356009f20206ca37a)
![{\displaystyle {\frac {2\nu (1-\nu )\Gamma ^{4}\left({\frac {\nu }{2}}\right)-24\Gamma ^{4}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}+}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f38cae09627de3f2065b670e153e31bea417c0c5)
![{\displaystyle +{\frac {8(2\nu -1)\Gamma ^{2}\left({\frac {\nu }{2}}\right)\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)}{\left[\nu \Gamma ^{2}\left({\frac {\nu }{2}}\right)-2\Gamma ^{2}\left({\frac {\nu +1}{2}}\right)\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2402e534ef694a1d0d26af95abc92d91ff0101b)








